Energía cinética en diferentes sistemas de referencia[editar]
Como hemos dicho, en la
mecánica clásica, la energía cinética de una masa puntual depende de su
masa 
y sus componentes del movimiento. Se expresa en
julios (J). 1 J = 1 kg·m
2/s
2. Estos son descritos por la
velocidad 
de la masa puntual, así:



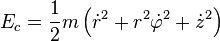
![E_c=\frac{1}{2}m \left(r^2 \left[\dot \theta^2 + \dot \varphi^2 \sin^2\theta \right] + \dot r^2 \right)](http://upload.wikimedia.org/math/1/b/6/1b63189e3cca32b06f6f4ede5a1bf61b.png)
Con eso el significado de un punto en una coordenada y su cambio temporal se describe como la
derivada temporal de su
desplazamiento:
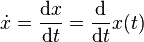
En un formalismo
hamiltoniano no se trabaja con esas componentes del movimiento, o sea con su velocidad, sino con su
impulso 
(cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:

Energía cinética de sistemas de partículas[editar]
Para una partícula, o para un sólido rígido que no este rotando, la energía cinética cae a cero cuando el cuerpo para. Sin embargo, para sistemas que contienen muchos cuerpos con movimientos independientes, que ejercen fuerzas entre ellos y que pueden (o no) estar rotando, esto no es del todo cierto. Esta energía es llamada 'energía interna'. La energía cinética de un sistema en cualquier instante de tiempo es la suma simple de las energías cinéticas de las masas, incluyendo la energía cinética de la rotación.
Un ejemplo de esto puede ser el
Sistema Solar. En el centro de masas del sistema solar, el Sol está (casi) estacionario, pero los planetas y planetoides están en movimiento sobre él. Así en un centro de masas estacionario, la energía cinética está aún presente. Sin embargo, recalcular la energía de diferentes marcos puede ser tedioso, pero hay un truco. La energía cinética de un sistema de diferentes marcos inerciales puede calcularse como la simple suma de la energía en un marco con centro de masas y añadir en la energía el total de las masas de los cuerpos que se mueven con velocidad relativa entre los dos marcos.
Esto se puede demostrar fácilmente: sea V la velocidad relativa en un sistema k de un centro de masas i:
Donde:
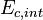 , es la energía cinética interna respecto al centro de masas de ese sistema
, es la energía cinética interna respecto al centro de masas de ese sistema es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas.
es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas. , es la masa total.
, es la masa total.
Por lo que la expresión anterior puede escribirse simplemente como:
1
Donde puede verse más claramente que
energía cinética total de un sistema puede descomponerse en su
energía cinética de traslación y la energía de
rotación alrededor del centro de masas. La energía cinética de un sistema entonces depende del
Sistema de referencia inercial y es más bajo con respecto al
centro de masas referencial, por ejemplo, en un sistema de referencia en que el centro de masas sea estacionario. En cualquier otro sistema de referencia hay una energía cinética adicional correspondiente a la masa total que se mueve a la velocidad del centro de masas.
Energía cinética de un sólido rígido en rotación[editar]
Para un sólido rígido que está rotando puede descomponerse la energía cinética total como dos sumas: la energía cinética de traslación (que es la asociada al desplazamiento del centro de masa del cuerpo a través del espacio) y la energía cinética de rotación (que es la asociada al movimiento de rotación con cierta velocidad angular). La expresión matemática para la energía cinética es:
Donde:
 Energía de traslación.
Energía de traslación.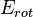 Energía de rotación.
Energía de rotación. Masa del cuerpo.
Masa del cuerpo. tensor de (momentos de) inercia.
tensor de (momentos de) inercia. velocidad angular del cuerpo.
velocidad angular del cuerpo. traspuesta del vector de la velocidad angular del cuerpo.
traspuesta del vector de la velocidad angular del cuerpo. velocidad lineal del cuerpo.
velocidad lineal del cuerpo.
El valor de la energía cinética es positivo, y depende del
sistema de referencia que se considere al determinar el valor (módulo) de la velocidad

y

. La expresión anterior puede deducirse de la expresión general:
Energía cinética en mecánica relativista[editar]
Energía cinética de una partícula[editar]
Si la velocidad de un cuerpo es una fracción significante de la
velocidad de la luz, es necesario utilizar
mecánica relativista para poder calcular la energía cinética. En
relatividad especial, debemos cambiar la expresión para el
momento lineal y de ella por interacción se puede deducir la expresión de la energía cinética:
Tomando la expresión relativista anterior, desarrollándola en
serie de Taylor y tomando únicamente el término

se recupera la expresión de la energía cinética típica de la
mecánica newtoniana:
2
Se toma únicamente el primer término de la serie de Taylor ya que, conforme la serie progresa, los términos se vuelven cada vez más y más pequeños y es posible despreciarlos.
La ecuación relativista muestra que la energía de un objeto se acerca al infinito cuando la velocidad
v se acerca a la velocidad de la luz
c, entonces es
imposible acelerar un objeto a esas magnitudes. Este producto matemático es la fórmula de
equivalencia entre masa y energía, cuando el cuerpo está en reposo obtenemos esta ecuación:
Así, la energía total E puede particionarse entre las energías de las masas en reposo más la tradicional energía cinética newtoniana de baja velocidad. Cuando los objetos se mueven a velocidades mucho más bajas que la luz (ej. cualquier fenómeno en la tierra) los primeros dos términos de la serie predominan.
La relación entre energía cinética y
momentum es más complicada en este caso y viene dada por la ecuación:
Esto también puede expandirse como una
serie de Taylor, el primer término de esta simple expresión viene de la mecánica newtoniana. Lo que sugiere esto es que las fórmulas para la energía y el momento no son especiales ni axiomáticas pero algunos conceptos emergen de las ecuaciones de masa con energía y de los principios de la relatividad.
Energía cinética de un sólido en rotación[editar]
A diferencia del caso clásico la energía cinética de rotación en mecánica relativista no puede ser representada simplemente por un
tensor de inercia y una expresión cuadrática a partir de él en el que intervenga la
velocidad angular. El caso simple de una esfera en rotación ilustra este punto; si suponemos una esfera de un material suficientemente rígido para que podamos despreciar las deformaciones por culpa de la rotación (y por tanto los cambios de densidad) y tal que su velocidad angular satisfaga la condición
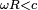
se puede calcular la energía cinética

a partir de la siguiente integral:
Integrando la expresión anterior se obtiene la expresión:
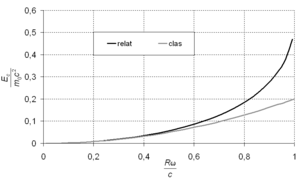
Comparación entre la expresión para la energía cinética de una esfera de acuerdo con la
mecánica clásica y la
mecánica relativista (aquí
R es el radio, ω la velocidad angular y
m0 la masa en reposo de la esfera.
Para una esfera en rotación los puntos sobre el eje no tienen velocidad de traslación mientras que los puntos más alejados del eje de giro tienen una velocidad

, a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación:
Paradójicamente, dentro de la teoría especial de la relatividad, el supuesto de que es posible construir un sistema rotar progresivamente más rápido un esfera sobre su eje, lleva a que los puntos más alejados del eje de giro alcancen la velocidad de la luz aplicando al cuerpo una cantidad finita de energía
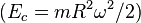
. Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.
Energía cinética en mecánica cuántica[editar]
En la
mecánica cuántica, el valor que se espera de energía cinética de un
electrón,
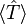
, para un sistema de electrones describe una
función de onda 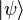
que es la suma de un electrón, el operador se espera que alcance el valor de:
donde
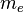
es la masa de un electrón y
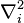
es el
operador laplaciano que actúa en las coordenadas del electrón
iésimo y la suma de todos los otros electrones. Note que es una versión cuantizada de una expresión no relativista de energía cinética en términos de momento:
El formalismo de la
funcional de densidad en mecánica cuántica requiere un conocimiento sobre la densidad electrónica, para esto formalmente no se requiere conocimientos de la función de onda.
Dado una densidad electrónica
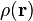
, la funcional exacta de la energía cinética del
n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:
donde
![T[\rho]](http://upload.wikimedia.org/math/b/0/3/b03e2e33686044e5f78fe6df092b3bd0.png)
es conocida como la funcional de la energía cinética de
Von Weizsacker.
Energía cinética de partículas en la mecánica cuántica[editar]
En la teoría cuántica una magnitud física como la energía cinética debe venir representada por un
operador autoadjunto en un espacio de Hilbert adecuado. Ese operador puede construirse por un proceso de
cuantización, el cual conduce para una partícula moviéndose por el espacio euclidiano tridimensional a una representación natural de ese operador sobre el
espacio de Hilbert 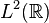
dado por:
que, sobre un dominio denso de dicho espacio formado clases de equivalencia representables por funciones
C², define un operador autoadjunto con
autovalores siempre positivos, lo cual hace que sean interpretables como valores físicamente medibles de la energía cinética.
Energía cinética del sólido rígido en la mecánica cuántica[editar]
Un sólido rígido a pesar de estar formado por un número infinito de partículas, es un sistema mecánico con un número finito de
grados de libertad lo cual hace que su equivalente cuántico pueda ser representado por sobre un espacio de Hilbert de dimensión infinita de tipo
L² sobre un
espacio de configuración de inútiles dimensión finita. En este caso el espacio de configuración de un sólido rígido es precisamente el
grupo de Lie SO(3) y por tanto el espacio de Hilbert pertinente y el operador energía cinética de rotación pueden representarse por:
donde

es la
medida de Haar invariante de
SO(3),
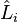
son los operadores del
momento angular en la representación adecuada y los escalares
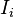
son los momentos de inercia principales.
Energía cinética y temperatura[editar]

















 Mecánica, por su parte, es algo que ejerce un mecanismo o aquello que puede provocar diversos efectos físicos, como una erosión o un choque. También se trata de la rama de la
Mecánica, por su parte, es algo que ejerce un mecanismo o aquello que puede provocar diversos efectos físicos, como una erosión o un choque. También se trata de la rama de la 
 y sus componentes del movimiento. Se expresa en
y sus componentes del movimiento. Se expresa en  de la masa puntual, así:
de la masa puntual, así: 

 ):
):
 ):
):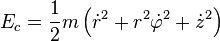
 ):
):![E_c=\frac{1}{2}m \left(r^2 \left[\dot \theta^2 + \dot \varphi^2 \sin^2\theta \right] + \dot r^2 \right)](http://upload.wikimedia.org/math/1/b/6/1b63189e3cca32b06f6f4ede5a1bf61b.png)
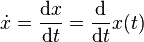
 (cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:
(cambio en la cantidad de movimiento). En caso de usar componentes cartesianas obtenemos:

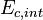 , es la energía cinética interna respecto al centro de masas de ese sistema
, es la energía cinética interna respecto al centro de masas de ese sistema es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas.
es el momento respecto al centro de masas, que resulta ser cero por la definición de centro de masas. , es la masa total.
, es la masa total.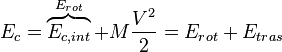
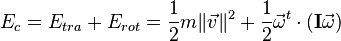
 Energía de traslación.
Energía de traslación. Energía de rotación.
Energía de rotación. Masa del cuerpo.
Masa del cuerpo.
 velocidad angular del cuerpo.
velocidad angular del cuerpo.
 velocidad lineal del cuerpo.
velocidad lineal del cuerpo. y
y  . La expresión anterior puede deducirse de la expresión general:
. La expresión anterior puede deducirse de la expresión general: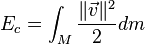
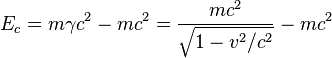
 se recupera la expresión de la energía cinética típica de la
se recupera la expresión de la energía cinética típica de la ![E_c = \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}-mc^2=
mc^2\left [\frac{1}{2}\left(\frac{v^2}{c^2}\right)+
\frac{3}{8}\left(\frac{v^2}{c^2}\right)^2+...\right] = \frac{1}{2}mv^2](http://upload.wikimedia.org/math/a/7/0/a707bed31a55d4d79c8be7b5e9db66a4.png)

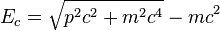
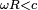 se puede calcular la energía cinética
se puede calcular la energía cinética  a partir de la siguiente integral:
a partir de la siguiente integral:
![E_c = \frac{3}{2}m_0c^2 \left(\frac{c}{R\omega}\right)^2
\left[ 1 + \frac{1}{2} \left(\frac{R\omega}{c}-\frac{c}{R\omega}\right)
\ln \left(\frac{c+R\omega}{c-R\omega} \right) \right]
- m_0c^2](http://upload.wikimedia.org/math/8/b/7/8b7a701ef31b6f0f0083d4d0260a4ca4.png)

 , a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación:
, a medida que esta velocidad se aproxima a la velocidad de la luz la energía cinética de la esfera tiende a crecer sin límite. Esto contrasta con la expresión clásica que se da a continuación: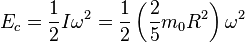
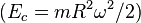 . Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.
. Lo cual revela que el supuesto no puede ser correcto cuando algunos puntos de la periferia del sólido están moviéndose a velocidades cercanas a la de la luz.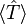 , para un sistema de electrones describe una
, para un sistema de electrones describe una 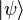 que es la suma de un electrón, el operador se espera que alcance el valor de:
que es la suma de un electrón, el operador se espera que alcance el valor de: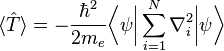
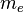 es la masa de un electrón y
es la masa de un electrón y 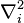 es el
es el 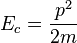
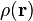 , la funcional exacta de la energía cinética del n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:
, la funcional exacta de la energía cinética del n-ésimo electrón es incierta; sin embargo, en un caso específico de un sistema de un electrón, la energía cinética puede escribirse así:![T[\rho] = \frac{1}{8} \int \frac{ \nabla \rho(\mathbf{r}) \cdot \nabla \rho(\mathbf{r}) }{ \rho(\mathbf{r}) } d^3r](http://upload.wikimedia.org/math/f/5/2/f527c2275e20ee9262c65527e0d16fe9.png)
![T[\rho]](http://upload.wikimedia.org/math/b/0/3/b03e2e33686044e5f78fe6df092b3bd0.png) es conocida como la funcional de la energía cinética de
es conocida como la funcional de la energía cinética de 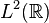 dado por:
dado por:
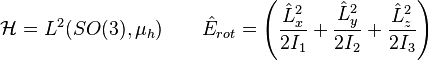
 es la
es la 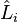 son los operadores del
son los operadores del 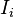 son los momentos de inercia principales.
son los momentos de inercia principales.
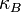 es la
es la 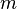 es la
es la